Kalman Filter

贝叶斯滤波讨论

前面我们介绍了贝叶斯滤波方法，在贝叶斯滤波方法中，两个重要过程

状态预测 $Bel(x_t) = \int P(x_t| x_{t-1}, u_t) Bel(x_{t-1}) dx_{t-1}$ 状态更新 $Bel(x_t) = \eta P(z_t|x_t) Bel(x_t)$ 假设$Bel(x_{t-1})$是任意分布，方程会比较难以求解，针对这种情况，可以考虑用蒙特卡罗方式求解，也即粒子滤波算法，这里不讨论粒子滤波算法。假设$Bel(x_t)$服从高斯分布，可以直接用分布的均值和方差来表示分布。这就会比较容易处理了。

高斯分布

一元高斯分布：

$p(x) \sim N(\mu, \sigma^2)$ $p(x) = \frac {1} {\sqrt {2 * \pi}\sigma} e^{-\frac{1}{2} \frac{(x-\mu)^2}{\sigma^2}}$

其中，$\mu$和$\sigma^2$分别表示期望和方差。

多元高斯分布： $p(\mathbb x) \sim N( \boldsymbol {\mu}, \Sigma)$ 其中，$\boldsymbol{\mu}, \Sigma$分别表示均值，协方差矩阵。
假设$\mathbb x \sim N(\boldsymbol{\mu}, \Sigma$,则对于线性变换$\mathbb y =A \mathbb x+B$有， $\mathbb y\sim N(A \boldsymbol{\mu} + B, A\Sigma A^T)$
假设$ x_1 \sim N( {\mu_1}, \sigma_1^2), x_2 \sim N( {\mu_2}, \sigma_2^2)$，$ x_1, x_2$相互独立，对于线性组合$y = x_1 + x_2$有， $y \sim N( {\mu_1} + {\mu_2}, \sigma_1^2 + \sigma_2^2 + 2\rho\sigma_1\sigma_2)$
假设$ x_1 \sim N( {\mu_1}, \sigma_1^2), x_2 \sim N( {\mu_2}, \sigma_2^2)$，$x_1, x_2$相互独立，则$p(x_1) P(x_2)$： $p( x_1) p( x_2) \sim N(\frac {\sigma_2^2} {\sigma_1^2+\sigma_2^2} \mu_1 + \frac {\sigma_1^2} {\sigma_1^2+\sigma_2^2} \mu_2, \frac {\sigma_1^2 \sigma_2^2} {\sigma_1^2+\sigma_2^2} )$

Kalman 滤波

符号约定

$\mathbb x_t$是一个n位向量，表示t时刻的状态的均值；
$P_t$是t时刻状态的协方差矩阵，是一个$n \times n$的矩阵；
$\mathbb u_t$表示t时刻模型的控制输入，是一个$m$维的输入；
$\mathbb z_t$表示t时刻模型的观测量，是一个$l$维的输入；
$A_t$表示状态由t-1时刻到t时刻的转移矩阵，是一个$n \times n$的矩阵；
$B_t$表示从控制量到状态量的转移矩阵，是一个$n \times m$的矩阵；
$H_t$表示从状态到观测的转换矩阵，是一个$l \times n$的矩阵；
$R_t, Q_t$分别表示观测噪声矩阵和过程噪声矩阵，大小分别是$l \times l, n \times n$

基本假设

系统状态方程是线性的；
观测方程是线性的；
过程噪声符合零均值高斯分布的；
观测噪声符合零均值高斯分布的；

对于某系统，假设其状态方程为： $\mathbb x_t = A_t \mathbb x_{t-1} + B_t \mathbb u_t + \epsilon_t$ 观测方程为： $\mathbb z_t = H_t \mathbb x_t + \delta_t$ 滤波算法

预测过程

根据假设，状态，误差都是服从高斯分布的，根据状态方程，易得

t时刻均值为： $\mathbb x_t = A_t \mathbb x_{t-1} + B_t \mathbb u_t$ t时刻方差为： $P_t = A_t P_{t-1} A_t^T + Q_t$ 从贝叶斯角度推算有 $P(\mathbb x_t| \mathbb x_{t-1}, u_t) \sim N(A_t \mathbb x_t + B_t \mathbb u_t, Q_t)$ 所以预测方程有 ${Bel(\mathbb x_t)} = \int p(\mathbb x_t | \mathbb x_{t-1}, \mathbb u_t) Bel(\mathbb x_{t-1}) d\mathbb x_{t-1}$

此过程为两个高斯分布的卷积，具体可查阅相关推导文献，这里不赘述，可得： ${Bel(x_t)} = \begin{cases} \mathbb x_t = A_t \mathbb x_{t-1} + B_t \mathbb u_t \\ P_t = A_tP_{t-1}A_t^T + Q_t\end{cases}$
更新过程

从贝叶斯滤波角度看有： $P(z_t|x_t) \sim N(H_t \mathbb x_t, Q_t)$
$Bel(x_t) \sim N(\mathbb x_t, P_t)$
所以有 $Bel(\mathbb x_t) = \eta P(z_t|x_t) Bel(x_t)$ 此过程为两个高斯分布的求积过程，可得 $Bel(\mathbb x_t) = \begin{cases} \mathbb x_t = \mathbb x_t + K_t(\mathbb z_t - H_t \mathbb x_t) \\ P_t = (I - K_t H_t)P_t \end{cases} 其中， K_t = P_t H_t^T(H_tP_tH_t^T + R_t)^{-1}$ 由此可有卡尔曼滤波的五条公式：

Prediction: $\mathbb x_t = A_t \mathbb x_{t-1} + B_t \mu_t \\ P_t = A_t P_t A_{t-1}^T + Q_t$ Update: $K_t = P_tH_t^T(H_tP_tH_t^T + R_t)^{-1} \\ \mathbb x_t = \mathbb x_t + K_t (\mathbb z_t - H_t \mathbb x_t) \\ P_t = (I-K_tH_t)P_t$ 更新部分，还可以用另外的形式表示：

首先计算观测值与预测值的残差有： $Residual_t = \mathbb z_t - H_t \mathbb x_t$ 然后计算观测值的协方差： $S_t = H_tP_tH_t^T + R_t$ 增益(权重)系数： $K_t = P_t H_t^T S_t^{-1}$ $H_t$将状态空间转到观测空间，增益系数近似于两者的比值，所以基于增益系数有， $\mathbb x_t = \mathbb x_t + K_t Residual_t$
$P_t = P_t - P_t H_t^T S_t^{-1}H_t P_t$
这里着重解释下$K_t$，前面说了$K_t$是两者的比值，也就是如果$K_t$越小，则说明，观测的误差越大，这样估计值更靠近预测值，反之如果观测误差越小，则$K_t$越大，估计值就更靠近观测值。

应用举例

假设有一机器人在一平面上运动，其状态可表述为$(x, y, v_x, v_y)$，分别是机器人当前位置，$x$和$y$方向上的速度值。机器人运动模型为： $\begin{cases} x_{t+1} = x_t + v_x * dt \\ y_{t+1} = y_t + v_y * dt \\ v_x = v_x + a_x * dt \\ v_y = v_y + a_y * dt \end{cases}$ 其中$a_x, a_y$分别是输入的控制量。机器人的控制周期是0.1s, 也即$dt = 0.1$。机器人携带了一个感知当前位置的传感器，每0.1s能给出当前的位置。现在估计机器人每个时刻的坐标。

式（27）写成乘法的形式： $\mathbb x_{t+1} = \begin{pmatrix} 1. & 0. & 1. & 0. \\ 0. & 1. & 0. & 1. \\ 0. & 0. & 1. & 0. \\ 0. & 0. & 0. & 1. \end {pmatrix} \mathbb x_t + \begin {pmatrix} 0. & 0. \\ 0. & 0. \\ 1. & 0. \\ 0. & 1. \end {pmatrix} \mathbb u_t$ 其中$\mathbb x_t = (x, y, v_x, v_y)^T, \mathbb u_t = (a_x, a_y)^T$。

仿真实现该系统，具体文件可参考src/filter/kalman_filter.py文件：

a. 首先实现机器人仿真部分

class Robot(object):
    def __init__(self, x=0.0, y=0.0):
        self.x = 0.0
        self.y = 0.0
        self.v_x = 0.0
        self.v_y = 0.0
        self._process_variance = np.diag([0.5, 0.5]) ** 2 # 设置实际的执行误差
        self._observe_variance = np.diag([0.5, 0.5]) ** 2 # 设置实际的观测误差
   
    def move(self, a_x = 1., a_y = 1., dt=0.1):
        a_x = a_x + np.random.randn() * self._process_variance[0, 0]
        a_y = a_y + np.random.randn() * self._process_variance[1, 1]
        self.x = self.x + self.v_x * dt
        self.y = self.y + self.v_y * dt
        self.v_x = self.v_x + a_x * dt
        self.v_y = self.v_y + a_y * dt
   
    def observe(self):
        x = self.x + np.random.randn() * self._observe_variance[0, 0]
        y = self.y + np.random.randn() * self._observe_variance[1, 1]
        return x, y
   
    def get_true_state(self):
        return self.x, self.y

b. 滤波估计机器人位置

class KFEstimator(object):
    def __init__(self, x, y, vx, vy, P):
        self.X = np.matrix([x, y, vx, vy]).T
        self.P = P
   
    def predict(self, u, Q, dt=0.1):
        A = np.matrix([ [1., 0., dt, 0. ],
                        [0., 1., 0., dt ],
                        [0., 0., 1., 0. ],
                        [0., 0., 0., 1. ]])
        B = np.matrix([ [0., 0.],
                        [0., 0.],
                        [dt, 0.],
                        [0., dt]])
        self.X = A * self.X + B * u
        self.P = A * self.P * A.T + Q
        return self.X
   
    def update(self, z, R):
        H = np.matrix([ [1., 0., 0., 0.],
                        [0., 1., 0., 0.]])
        residual = z - H*self.X
        S = H * self.P * H.T + R
        K = self.P * H * np.linalg.inv(S)
   
        self.X = self.X + K * residual
        self.P = self.P - K * H * self.P
        return self.X

c. 结果分析

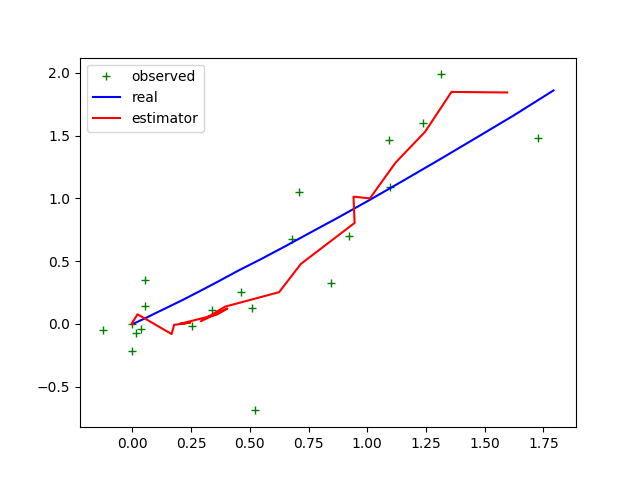
对比不同的观测方差矩阵和过程观测方差矩阵。待补充。

不同频率融合处理

前面分析了，传感器观测周期和机器人的执行周期相同，如果两个周期不同要怎么处理，也就是如何处理频率不同带来的问题？

通常从五条公式上，预测完之后就做更新，实际上没必要。

观测本质上是对预测分布的纠正，所以预测之后不一定就是更新操作，两个过程是独立进行的，也即是哪个数据先到来就先做哪一部分。

todo不同频率处理的过程分析

todo 传感器数据处理延时高于数据读取频率，如何处理？

多传感器融合处理

Reference

细说Kalman滤波器