车辆运动学模型

自行车模型

自行车模型简化了车辆的运动学模型，通常适用于低速场景下的车辆控制。自行车模型只考虑前后两轮，并且不考虑车辆的测滑，车辆的转向由前轮控制，后轮驱动速度。下面简要讨论自行车模型：

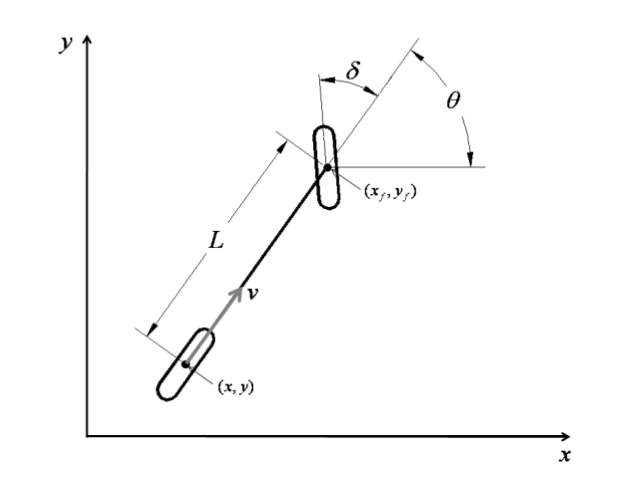
上图是自行车运动学的示意图，其中$(x_f, y_f)和(x, y)$分别是车辆的前轮坐标和后轮坐标，$L$是轴距，$\theta$是车辆的航向角，$\delta$是车辆的前轮抓角。

在自动驾驶控制中，通常会研究车辆的运动学方程，也即如何由当前状态推演到下一个状态，而这个过程也可以考虑为函数的泰勒展开。

假设在$\Delta t$时间内，车辆在$x$方向的变化量为$\dot{x}$，在$y$方向的变化量为$\dot{y}$，

根据刚体的运动约束，我们可以得到如下几条公式： $\dot{x_f} \sin(\theta + \delta) = \dot{y_f}cos(\theta + \delta)$

$$\dot{x} \sin(\theta) = \dot{y} \cos(\theta)$$

根据$x_f, y_f$和$x,y$之间的关系， $x_f = x + L\cos(\theta) \\ y_f = y + L \sin(\theta)$ 消除$x_f, y_f$有， $$ \begin {align*} 0 &= \dot{x_f} \sin(\theta + \delta) - \dot{y_f} \cos(\theta + \delta)
&= \frac{\nabla(x+L\cos(\theta))} {\nabla t} \sin(\theta + \delta) - \frac{\nabla (y+L\sin(\theta))}{\nabla t} \cos(\theta + \delta)
&= (\dot{x} - \dot{\theta} L \sin(\theta)) \sin(\theta + \delta) - (\dot{y} + \dot{\theta} \cos(\theta)) \cos(\theta + \delta)
&= \dot{x} \sin(\theta + \delta) - \dot{y} \cos(\theta+\delta)
&- \dot{\theta} L \sin(\theta) (\sin(\theta)\cos(\delta) + \sin(\delta)\cos(\theta))
&- \dot{\theta} L \cos(\theta)(\cos(\theta)\cos(\delta) - \sin(\delta)\sin(\theta))
&= \dot{x} \sin(\theta + \delta) - \dot{y} \cos(\theta+\delta) - \dot{\theta}L \cos(\delta)

\end {align} \tag{4} $也即是:$ \dot{x}\sin(\theta + \delta) - \dot{y}\cos(\theta + \delta) - \dot{\theta} L \cos(\delta) = 0 $对于后轮有：$ \dot{x} = v \cos(\theta)
\dot{y} = v \sin(\theta) $带入(4)有$ \dot{\theta} = \frac {v \tan(\delta)}{L} $根据(6)，以及曲率的公式，有$ \begin{align} R = \frac {v} {\dot \theta}
\frac {v \tan(\delta)} {L} = \frac{v}{R}
\tan{\delta} = \frac {L} {R} \end{align*} \tag 7 $$ (7)式用于pure-pursuit中。

我们将(5), (6)用增量方程表示： $\begin{bmatrix} \dot x \\ \dot y \\ \dot \theta \\ \dot \delta \end{bmatrix} = \begin{bmatrix} \cos(\theta) \\ \sin(\theta) \\ \frac{\tan(\delta)}{L} \\ 0 \end{bmatrix} v + \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1\end{bmatrix} \dot{\delta} \tag 8$ 或者， $\begin{bmatrix} \dot x \\ \dot y \\ \dot \theta \\ \dot \delta \\ \dot v \end{bmatrix} = \begin{bmatrix} 0 \quad 0 \quad 0 \quad 0 \quad \cos(\theta) \\ 0 \quad 0 \quad 0 \quad 0 \quad \sin(\theta) \\ 0 \quad 0 \quad 0 \quad 0 \quad \frac {\tan(\delta)} {L} \\ 0 \quad 0 \quad 0 \quad 0 \quad 0 \\ 0 \quad 0 \quad 0 \quad 0 \quad 0 \end{bmatrix} \begin{bmatrix} x \\ y \\ \theta \\ \delta \\v \end{bmatrix} + \begin{bmatrix} 0 \quad 0 \\ 0 \quad 0 \\ 0 \quad 0 \\ 1 \quad 0 \\ 0 \quad 1 \\ \end{bmatrix} \begin{bmatrix} \gamma \\ a \end{bmatrix} \tag 9$ 其中，$\gamma, a$分别表示前轮转角的速率和加速度，或者 $\begin{bmatrix} \dot x \\ \dot y \\ \dot \theta \\ \dot v \end{bmatrix} = \begin{bmatrix} 0 \quad 0 \quad 0 \quad \cos(\theta) \\ 0 \quad 0 \quad 0 \quad \sin(\theta) \\ 0 \quad 0 \quad 0 \quad 0 \\ 0 \quad 0 \quad 0 \quad 0 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ \theta \\ v \end{bmatrix} + \begin{bmatrix} 0 \quad 0 \\ 0 \quad 0 \\ 1 \quad 0 \\ 0 \quad 1 \\ \end{bmatrix} \begin{bmatrix} \gamma \\ a \end{bmatrix} \tag {10}$ 根据增量方程，可以比较容易的推出下一个时刻的状态，假设车辆状态可以用$\mathbb x(t)$表示，则， $\mathbb x(t+1) = \mathbb x(t) + \dot {\mathbb x}(t) * \Delta t \tag{11}$ 基于式(11)，我们可以得到各类方程，一种常用的方程： $\begin{bmatrix} x(t+1) \\ y(t+1) \\ \theta(t+1) \\ v(t+1) \end{bmatrix} = \begin{bmatrix} 1 \quad 0 \quad 0 \quad \cos(\theta(t)) dt \\ 0 \quad 1 \quad 0 \quad \sin(\theta(t)) dt \\ 0 \quad 0 \quad 1 \quad 0 \\ 0 \quad 0 \quad 0 \quad 1 \end{bmatrix} \begin{bmatrix} x(t) \\ y(t) \\ \theta(t) \\ v(t) \end{bmatrix} + \begin{bmatrix} 0 \quad 0 \\ 0 \quad 0 \\ 1 \quad 0 \\ 0 \quad 1 \end{bmatrix} \begin{bmatrix} \delta(t) \\ a(t)\end{bmatrix} \tag{12}$ 当然根据状态表示的不同，可以得到不同的状态方程。

Path Coordinate

大部分时候，我们可以直接在全局坐标系下，做控制，但是有些情况下，需要在路径坐标下做控制。

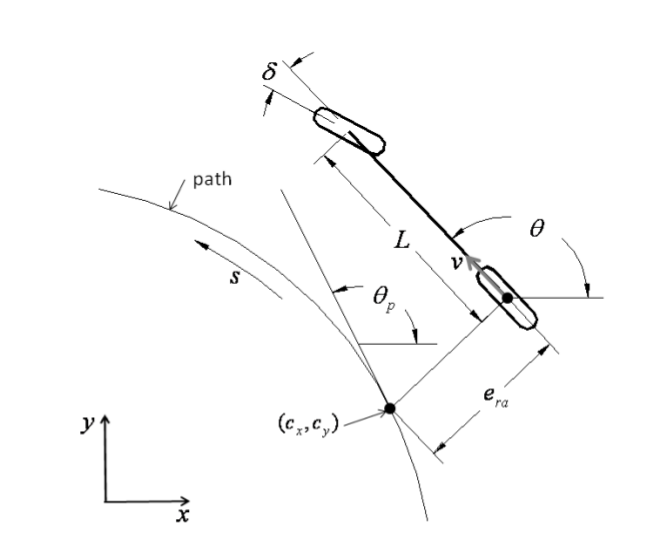
如图所示，$\theta$是车辆的航向角，$\theta_p$是车辆最近点P$(c_x, c_y)$的切线角度，$e_{ra}$是横向距离误差。对于轨迹，可以将$\theta_p$表示关于距离s的函数。

定义方向误差$\theta_e$，且有 $\theta_e = \theta_p(s) - \theta \tag{13}$ 根据曲率计算公式，有： $k_p = \frac {d \theta_p(s)} {ds} \tag{14}$ 也即是 $\dot \theta_p(s) = k_p \dot s \tag{15}$ 我们先看$e_{ra}$的增量，: $\dot e_{ra} = v \sin(\theta_e) \tag{16}$ 接下来，我们计算$\dot s$，s的计算需要回到x-y坐标系下。我们知道在$\Delta t$时间内，车辆水平方向移动的距离为$v \cos(\theta)$，所以根据p点的切线方向有： $\begin{align*} \dot s &= v\ cos(\theta) \sqrt{1 + \tan^2(\theta_p(s))} \\ &= \frac {v \cos(\theta) } { \cos(\theta_p(s) ) } \\ &= \frac {v \cos(\theta_p(s) + \theta_e)} { \cos(\theta_p(s)) } \\ &= \frac {v \cos (\theta_p(s))\ cos(\theta_e) + v\sin(\theta_p(s)) \sin(\theta_e))} {cos(\theta_p(s))} \\ &= v\cos(\theta_e) + v \sin(\theta_e) \tan( \theta_p(s)) \\ &= v\cos(\theta_e) + \dot \theta_p(s) \dot(e_{ra}) \end{align*} \tag {17}$ 也即是 $\dot s = v \cos(\theta_e) + \dot e_{ra} \dot \theta_p(s) \tag {18}$ 1根据式(15)和式(17)，可得 $\dot s = \frac {v cos(\theta_e)} {1 - \dot e_{ra} k(s)} \tag{19}$ 所以如果将状态表示为$(s, e_{ra}, \theta_e)$，我们可得增量方程为： $\begin{bmatrix} \dot s \\ \dot e_{ra} \\ \dot \theta_e \\ \dot \delta \end{bmatrix} = \begin{bmatrix} \frac {\cos(\theta_e)} {1 - \dot e_{ra} k(s)} \\ \sin(\theta_e) \\ \frac {tan(\delta)} {L} - \frac{k(s)\cos(\theta_e)}{1 - \dot e_{ra} k(s)} \\ 0 \end {bmatrix} v + \begin{bmatrix} 0 \\ 0 \\0 \\ 1 \end{bmatrix} \dot {\delta} \tag{20}$ 有了状态方程之后，我们就可以考虑使用MPC或者LQR计算车辆控制了。

reference

1. Automatic Steering Methods for Autonomous Automobile Path Tracking
2. Improved Trajectory Planning for On-Road Self-Driving Vehicles Via Combined Graph Search, Optimization & Topology Analysis